Hyperparameter Optimization
Many of the machine learning models have hyperparameters, i.e., configurations of the model that we decide before training a model. For example, the number of hidden states in a Gaussian Mixture Hidden Markov Model, the number of trees in a random forest, or the number of neurons in each layer of a neural networks.
Grid Search
Grid search lists all the combinations of the paramters and train model for each to find the best. Take Gaussian Mixture HMM for example. It has paramters to set such as the number of hidden states, the number of Gaussian components in the mixture model for each state, and the number of iterations for training the model. Let's say we have the following paramters to try.
- The number of hidden states: 2, 3, 4
- The number of Gaussian components in the mixture model for each state: 3, 4, 5
- The number of iterations for training the model: 10, 20, 30
Bayesian optimization
Instead of blindly testing all combinations, we can use advanced algorithms like Bayesian optimization. The idea is that as we observe more of model performances, we become more confident about the performance around those observations. Using a method like Gaussian Process, we can make a prediction of the model performance at different parameter values. Confidence around the known data points will be narrow while it would be wider at unexplored areas.
For example, let's say model performance was 20, 32, and 5 when we set a model paramter to 2, 3, and 5. We then have (paramter, performance) pairs of (2, 20), (3, 32), and (5, 5) in our knowledge. Gaussian Process then tell us predicted model performances, expressed as confidence intervals, at different parameter values.
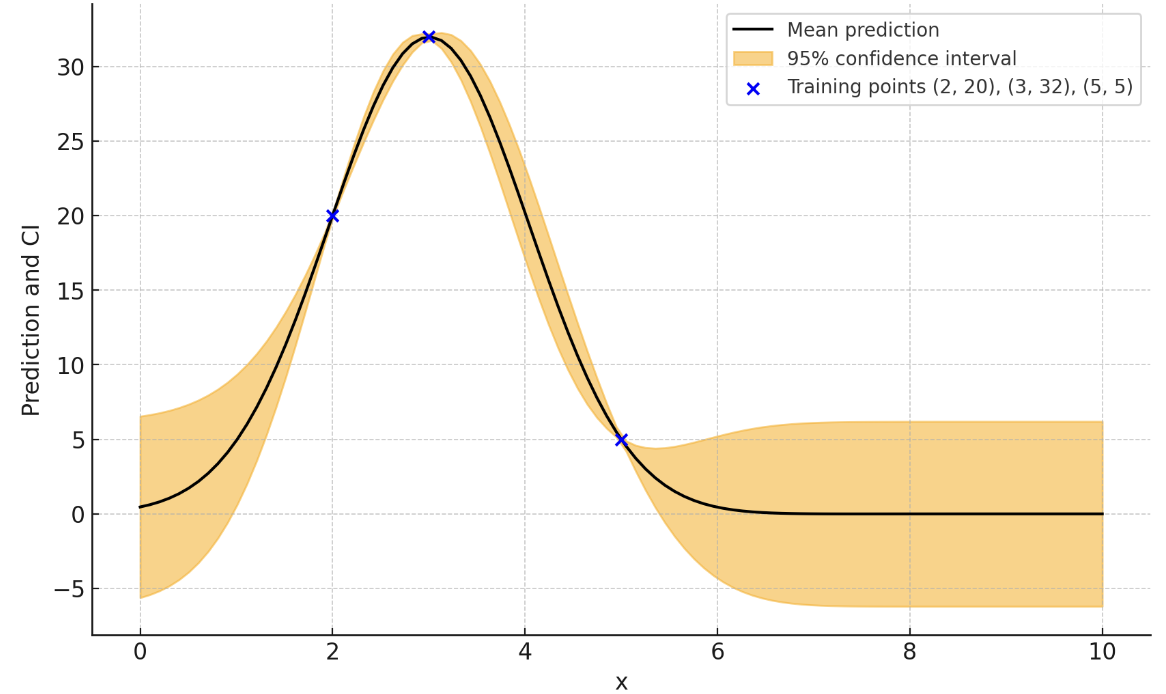
Example of Bayesian Optimization after finding model performances at 2, 3, and 5.
Based on such knowledge, at each step towards finding the best parameters, we can choose between exploit (trying the most promising parameter) or explore (trying new parameters). Balancing the two, bayesian optimization is able to find the best parameters efficiently.