Hidden Markov Models (HMM)
One of the well known machine learning algorithms in the sequential data analysis is Hidden Markov Model (HMM). It has been one of the popular algorithms used in speech recognition, handwriting recognition, and time series analysis.
Hidden Markov Model (HMM) are a type of probabilistic model. It assumes that the data is generated by unobserved (hidden) states while we can only observe the outputs from the states.
Imagine there are two urns, one with 10 red balls and 5 blue balls, and the other with 5 red balls and 10 blue balls. There's a person who picks one of the urns randomly and picks a ball from it.
A person picks a ball from one of the urns.
We only can observe the balls but not the urns. Problem that HMM (hidden markov model) solves is to infer the hidden states (urns) from the observed outputs (balls). This is useful in many applications such as speech recognition, handwriting recognition, and time series analysis. For example, in speech recognition, the hidden states are the words, and the observed outputs are the audio signals. From the audio, we infer the words.
During this process, HMM identifies multiple things:
- Probability of starting from a certain state
- Transition probability between states
- Emission probability of observing an output from a state
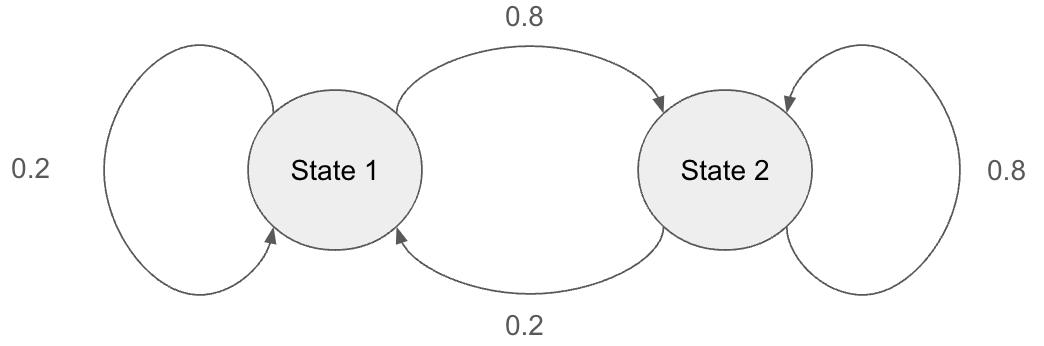
Two states $S_1$ and $S_2$ with transition probabilities annotated.
When applying HMM to the bitcoin price, we aim to infer the current state, which is hidden from us, from the price changes so far. After then, we infer the next state using the identified transition probability as well as the output from the emission probability.
Gaussian Mixture as the Output Distribution
In each state, HMM assumes that the output is generated from a specific distribution. For instance, if an urn contains 5 red balls and 10 blue balls, the probability of drawing a red ball is $5/15$ and the probability of drawing a blue ball is $10/15$. However, for continuous values like stock prices, we need a distribution that can more flexibly represent the data.
A Gaussian Mixture models a distribution as a combination of multiple Gaussian distributions (aka normal distributions or bell-shaped curves). It is powerful in representing complex distributions and can approximate any distribution given a sufficient number of components. Therefore, we use GMM to model the output distribution in each state.
A Gaussian Mixture Model with three Gaussian distributions
HMM for Air Passengers
To demonstrate the application of HMM, we apply it to the air passengers dataset.
In the following, Gaussian Mixture HMM with 10 hidden states and 3 mixture components is applied after Yeo Johnson transformation and first order difference. Since HMM doesn't have no specific methods to identify the regularity in the data other than the output probabilities, it's difficult to capture that. Therefore, we're observing somewhat disapponting results.
Applying HMM to bitcoin
Before applying HMM to the bitcoin price changes, we enrich the data by adding open, high, low, and close prices. The steps for predicting future price changes are as follows:
- Identify hidden states from the bitcoin price, especially the current state.
- Infer the next likely state from the current hidden state.
- Predict the likely output (price) of the next state.
- Repeat the process of inferring the next likely state and predicting the output.
Below is the HMM prediction. As one can see, it's performance isn't that great.