Decision Tree

Decision tree is a widely-used machine learning algorithm for both classification and regression tasks. Unlike time series models, such as ARIMA, decision trees do not assume any specific patterns in the data.

Intuitive and Interpretable

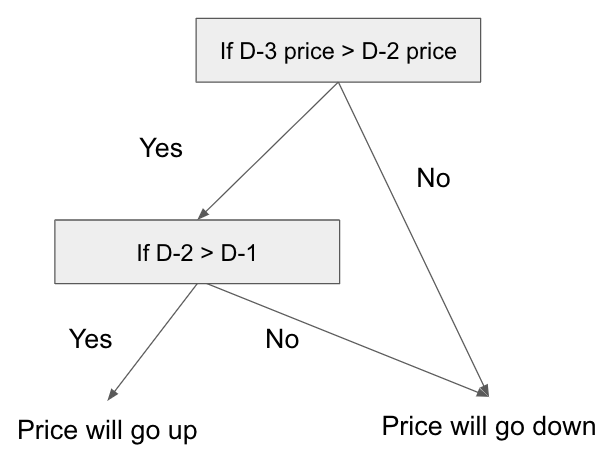
Decision trees are intuitive and easy to interpret models. They work by splitting the data into subsets based on feature values and making predictions based on the subset to which the data belongs. For example, consider a scenario where the price of Bitcoin increases only if it went up both the day before yesterday and yesterday. The decision tree for this scenario might look like the following:

Handles multiple features effectively

Each non leaf node in a decision tree can handle either categorical or continuous features, e.g., if x = "A", then go to left child node, otherwise go to right child node. Since each non leaf node's decision is after the parent node's, it's essentially a tree of complex if-else statements.

Thanks to such capability, exogenous data such as the NASDAQ-100 index can be seamlessly incorporated into the tree. Also, missing values (e.g., NaN or None) in features can be treated as a category of its own and used as node split criteria. In contrast, methods like ARIMA, which require non-missing values, fails with NaN or None.

Effectiveness

Despite the advancements in deep learning algorithms, decision trees and their ensemble methods often perform surprisingly well. For example, see this discussion on why tree-based models still outperform deep learning on typical tabular data.

Limitations

A decision tree assigns a constant value to leaf node, estimated from the training data. Therefore, if a certain high bitcoin price was never observed in the past, it's not possible for the tree to predict it. Also, decision tree is not designed to handle regularly happening events, such as the seasonality.

Above limitations makes the decision tree difficult to use for timeseries forecasting while ARIMA can handle them fairly well. This issue can be addresse by methods described in capturing trends and feature generation.

Overfitting

Decision trees are prone to overfitting, especially when the tree is deep. This can be mitigated by using ensemble methods such as random forests, or gradient boosting, or by limiting the depth of the tree.

Capturing complex regions

Making trees shallow does avoid overfitting, but it introduces the problem of rectangular splits. For instance, a node that splits on ((x > 100) and (y < 50))divides a region by drawing vertical and horizontal lines, and it cannot capture more complex regions like x^2 < y.

Decision tree for Air Passengers

To demonstrate model performance, we show the model's prediction results for the air passengers dataset. The cross validation process identified the best transformation to make the timeseries stationary and the optimal hyperparameters. The Root Mean Squared Error on the next day's closing price was used to determine the best model.

The chart below illustrates:

  1. train: training data
  2. prediction(train): the model's prediction for the training data periods
  3. test(input): test input data
  4. test(actual): test actual data
  5. prediction(test): the model's prediction on the selected days (1, 2, 7th days) of "test (actual)" periods given "test (input)".

Even with various efforts, the decision tree model appears to struggle in capturing the upward trend in the air passengers dataset. As a result, its predictions tend to be lower, and it's due to the lower values seen during the training period.